高等数学的一段公案

2024/12/22

最近儿子快要上高中。Twitter 上有些人在讨论教育。这些因素让我也回忆起以前自己上学的事情。我中学阶段也算优秀。初中自学完高中物理。高中尝试了两次学习高等数学。但是这两次都功亏一溃。怎么说功亏一溃呢？其实积分都学的差不多了，就差最后练习一些移项凑项的技巧，然后学会极坐标和多重积分就行了。而这些东西对于高一的我有巨大意义。因为我刚得过北京市物理奥林匹克竞赛二等奖，下一步就可以去参加需要微积分知识的高一级竞赛。

但就在这个时候我卡在了一个概念上。因为这个概念过不去，年少轻狂我就不去物理奥校了！当然那时候高考还是绝对的指挥棒，靠竞赛路径找好学校还不流行。不过回想起来也是草率的可以。

什么概念这么神奇呢？看下面这个式子：

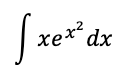
大多数有高数知识的人都能轻易解出来：

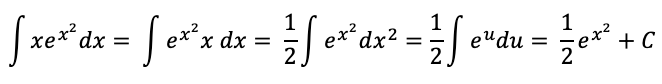
但这里隐藏了一个问题，就是第一步把 x 和 dx 结合了起来。而在大学微积分教材里明确写过：被积函数是一个整体，积分变量只是作为标记放在一旁。而另一方面，对于加法，会采用分配率：

所以一方面我们说 dx 不是一个因子，另一方面我们又在按照乘法的分配率和结合律来操作它。当我提出这个问题的时候，老师告诉我：你能算出答案就行了。我当时的信念就有些崩塌了。我也不是太形而上的人，但是高中就挺累的，如果没有点儿 bigger than life 的意义，我就丧失了额外求学的动力。

直到去年夏天因为各种因素不得不学习 machine learning 的时候，再次看到 chain rule of derivative，才豁然开朗。求第一个式子实际上是寻找 f(x) 满足：

但根据 chain-rule，我们也可以把想得到的答案形式改一下，变成寻找 f(g(x))，满足：

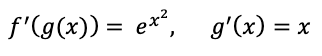
这个时候，我们对 g(x) 先求积分的形式，就等同于上面把 x 和 dx 先结合。虽然类似乘法操作，但是意义又不是乘法。回想起来当年就此放弃了高中时代对大学物理的早修，有点儿唏嘘。当年物理奥校是在人大附中，我每个周日从东直门骑车到了那里又不想去学，就到中关村闲逛，几年以后走上了程序员的道路。

发表在 未分类 | Leave a Comment »

职场的运作模型

2024/12/19

今天 Twitter 上有人诚心发布了一个问题：

下面的评论不出所料围绕产品经理的建议和程序员的回应是否中肯正确。可以说大多数人心目中的职场模型，是有一个客观的，可以让团队和产品最优化运营的状态。团队中每个人都应该为了揭示这个理想状态而参与讨论。凡是接近最优状态的建议，任何人都可以提出，团队则应无条件执行。

几乎每个即将或者刚刚走进职场的人，包括我自己，都被灌输了这样的模型。而且，在有些文化里，比如美国职场，这个模型是明面上辩论的唯一依据。当然这是另外一个话题。最终有些人会发现，这个模型和职场的现实之间差了一个重要的元素，团队成员的话语权和利益分配。

关于话语权和利益分配，我暂不定义。而是先假想这样一种状态。产品经理提出产品需求之后，在公开场合说我也理解要完成这个功能，开发团队最终可能要投入很多精力，所以我信任开发团队的成本评估，也相信他们会选择最好的方案。开发团队说，我理解这个功能对产品生命的意义，感谢产品经理。然后开发团队尽力重用现有的基础。事后产品经理说，非常欣赏开发团队节省开发资源的策略。这就是一个非常理想的话语权分配。每个角色都拥有了自己的话语权，同时用话语权获取了自己的利益。

下面假想另一种状态。产品经理提出需求之后，在私下甚至公开场合说，请开发团队尽量利用现有基础，不要重造车轮。开发团队针锋相对，说现有基础没办法完成需求。这就是不太好的情况，产品经理侵入了开发团队的话语权。开发团队就算委曲求全，最后做完，这个策略制定的 credit 也是由产品经理获得。

现实中，这两种情况之外还存在多种可能。比如说，产品经理尊重了开发团队的话语权，但是开发团队得寸进尺，对合理要求也声称需要超出实际的工程成本。

在职场的模型里，我不想说什么是「应该的」。甚至就连「侵入」别人话语权这样的概念，也并不绝对。因为每个角色的话语权，虽然有传统习惯的范围，也会随着博弈而改变。因为每个职场，都是一个利益分配的系统。其中的权力和利益分配都是市场和博弈的结果。但是身处其中的人，应该了解自己有没有侵入别的话语权，自己这么做了，什么人高兴，什么人不高兴。那些高兴和不高兴的人，反过来会不会让你高兴和不高兴。「为什么我说的话，他不听，是我说的不对还是他不讲道理？」你要知道有些话就不应该从你嘴里说出来。

换位思考的话，如果开发团队说现有的功能在用户的组合使用下就更好用。产品经理的需求是画蛇添足。那后者有多大的底线去客观思考对方意见的正确性。如果每个讨论都要思考这种正确性，那为什么还要有团队的分工。如果团队的分工是模糊的，那产品运营结果的利益分配要如何衡量？

话语权多还是少，让还是抢，这都没有正确和错误的答案。但错误的思考方式是去问「我说的对不对」，而不去考虑话语权这个因素。

发表在 未分类 | Leave a Comment »

Neither α nor Pre-multiplied

2023/09/26

在图像处理和图形学里 α-blending 是频繁被提到的概念。下图是 s 色层和 t 色层的 α-blending 过程示意。习惯称 s 色层在 t 色层「之上」。

和其它数学方法一样，可以视其为纯粹的 artificial 定义，由应用环境赋予其意义。但是我们也希望它能自然而然地表示某种物理意义，从而为它被广泛引用找到合理性。

上面的定义中，αs 的取值范围是 [0, 1]。为了分析合理的物理意义，先看取值范围的上界 αs = 1，代表 s 色层完全不透明。这时 α-blending 退化成实际世界中简单的「遮盖」现象。现在把 αs 减小。那么 t 色层会对 blending 结果贡献 Ct(1-αs)。这时我们可以理解为 s 色层有了 (1-αs) 的「透光度」，而自身的颜色减小为原来的 αs 倍。这里既然提到了色层的「自身颜色」，就解释一下物体颜色的物理意义。

颜色的意义

首先假设读者有 radiometry 的概念（如果没有也关系不大，很多东西可以非严格地直观理解）。Radiometry 的基本概念中，颜色是光线的属性，是光线的频谱能量分布，而非物体属性。当我们说「物体的」颜色，有两种情况：一是自发光物体，二是指物体表面的反射系数。后者真正呈现的颜色是整个 physically-based rendering 的话题，这里只非常简单地设定色层只有漫反射系数 [1]，在平行白光下 [2] 呈现的颜色在计算上类似自发光物体。

现在来看这种设定下 α 的意义。可以直观地认为光从色层的一面射入后有 (1-α) 的部分透过色层从另一面射出 [3]。我们设定这样一个场景：有一个完全不透明 (α = 1) 的色层，其漫反射系数为 C [4]。通过某种方式让它的 α 变为小于 1 的一个正数，其透明度变为为 (1-α)。那么问题在于是否有一种「自然合理」的基于单个 α 参数的物理模型，让它的漫反射系数同时变为 Cα。如果存在这种自然合理的模型，α-blending 的定义就更有意义。

统一 α 的困境

我们试图设计这样一个模型。首先假设半透明色层光学上「各向同性」，也就是说发生在其两个表面的光的作用完全相同。那么，s 色层能透过的 (1-αs) 的光就意味着它反射的光量减少到不透明色层的 αs 倍，等同于漫反射系数降低为 Csαs。这个分析合理吗？

我们先回顾 αs = 1 的完全不透明情况，这时反射系数 Cs 意味着色层「吸收了」(1-Cs) 部分的入射光线能量。那么，当某种方式让 αs 减小的时候，透过色层的光线不必非要从反射光线的衰减得到，也可以是部分的甚至全部的由避免「吸收」光线得到。所以，在直观的物理模型中，用 Csαs 表示半透明色层的漫反射系数并不能代表自然的物理意义，因为色层的漫反射系数和其透明度并没有单一的对应于 αs 的相互关系。完全可以说，半透明色层的漫反射系数应该是一个独立于 Cs 和 αs 的本源参数。

Pre-multiplied α-Blending

即便 α-blending 不能自然地符合某种简化的物理意义，能不能退一步说这不是个大问题？因为最简单的选择是把它完全当成一种「艺术效果」就好了。是吗？让我们看看下面的情况。

比如说，在软件中表示 s 和 t 两个图层 [5]，它们分别有 C 和 α 属性（称为 channel）。这时在屏幕上要把它们缩小为原尺寸的 1/3 然后按照 α-blending 重叠。从 α-blending 的数学定义可以看到，要正确 render 这种效果，有两种方法。一种是先按照原大小进行 blending，然后再 resize 结果。这种方法不但效率低，更严重的问题是它没办法处理两个色层有不同的偏移，旋转，和缩放比例的情况。另一种情况是对两个色层分别按照 screen 坐标进行 resample 之后进行「余下对应的」α-blending。但是这时要注意的是，为了结果正确，对 s 色层进行 resample 时，不能简单的对 Cs 和 αs 分别进行。而是需要对 Csαs 整体 resample。这个需求导致了实现方面的困难。今天的计算机架构中图形硬件对色层的通常实现是 texture，texture resample 的硬件实现是对各个 channel 分别独立进行。为了适应这种硬件约束，图形软件发展了一种概念，texture 的 color channel 中存储 Cα 的乘积而不是原来的 C，对此我们称为 C’。而「余下对应的」α-blending 变成：

这种方式称为 pre-multiplied α-blending。对应的 texture 的存储方式称为 pre-multiplied α channels。

从上面两节可以看到，已经存在自然的简化物理模型和硬件实现约束这两种情况大大削弱了 Csαs 中两个因子各自的意义。取而代之的是一个整体的 C’s。这里 C’s 或者可以看成是一个本源的物理属性，或者依然可以看成 Cs 和 αs两个因子的乘积。我们要注意的是，如果采用后一种解释，C’s 必须小于 Csαs，它的最大上限不能超过 1。

下文的讨论中我们会发现，从物理现象和硬件约束来看，对 C’s 的解释一般选用本源属性更加贴切。

真实物理意义

图层的 blending 效果其实很少局限在「半透明薄片」或者「纯艺术效果」这类设定，而是常用来模拟更真实的物理场景。下面例子中的两个图层，下面的是真实场景，上面的是 3D rendering 的结果。它们的 blending 结果包含四种物理场景。

这四种场景都符合下面的一般公式，只需要取不同的参数。而这个公式「恰好」和上面的 pre-multiplied α-blending 形式相同。

简单遮盖不用太多讨论。半透明遮盖很类似前面讨论的薄片色层。它对背景颜色的减去 αs 倍。但前景 s 图层的颜色 C’s 不再仅仅是漫反射参数，而是包括了 specular 反射的 rendering 结果。真实半透明物体最终反射的光线的颜色可以是任意正数 (超过屏幕动态范围的部分会被最终 clip)。阴影是对背景图层颜色的降低，降低程度为 αs。阴影部分前景图层的颜色 C’s = 0。反射是对背景图层颜色的增加。因为对背景颜色没有降低所以 αs = 0。前景图层 C’s 是反射的 rendering 结果。同一区域有可能同时拥有半透明、阴影和反射效果。

在这四种情况下，虽然图层 blending 的公式和 pre-multiplied α-blending 相同，但是意义相差很大。因为：

  • 在这个例子的 blending 中 C’s 的取值范围是任意正数。而 pre-multiplied α-blending 对C’s 的取值限制 [0, Csαs]，上限为 1 [6]。
  • 在这个例子的 blending 中 C’s 没有对应任何 Csαs 乘积的意义。

避之不及的 α 术语

总结上面的讨论就是，实际常用的图层 blending，特别是模拟真实场景效果的 blending 符合公式：

尽管该式和 pre-multiplied α-blending 形式相同，但是它的意义完全不同于后者。

如此说来，就给这种 blending 起个名字，比如叫 r-blending。然后在应用它的场景不再提及 α-blending 就好。是的，这是我写这篇 blog 想说的第一个提议。但这个避免提及 α 的提议的第一个问题是毕竟公式里依然存在 α。也许依然有人想把它归为 α-blending 的变种（但我不属于这个人群）。对此我要说，至少不要让这种形式和 pre-multipilied 这个词有任何瓜葛。

但是，即便如此，还有一个绕不过去的生态问题。大多数用户进行图层 blending 的工具是 Photoshop（或者完全遵循 Photoshop 概念的类似工具）。Photoshop 只支持 α-blending。它并不支持我们说的 r-blending，它的内部数据表示也不支持 pre-multiplied α。Photoshop 唯一处理 pre-multiplied α 的地方是 file import，它会把所有标为 pre-multiplied α 的文件的 color channels 在 import 时转换为 unmultiplied 的内部表示。

所以一个工具要生成能在 Photoshop 里进行 r-blending 的图层就要做些特殊处理。比如上面的 rendering 结果，虽然和 pre-multiplied 没有任何关系，但是为哄骗 Photoshop 去做我们想要的工作，存储这个 rendering 结果到文件的时候要把它 tag 成 pre-multiplied-α 数据。这样 Photoshop 在打开文件的时候，会把每个 color channel 除以 α-channel [7]。然后 blending 的时候再乘回去。前后做了一些无用功但是结果也还大致正确 [8]。但并不总是。

因为上面提到，renderer 的结果会有以下两种情况：

  • α-channel 为零。比如反射现象。在这种情况下，Photoshop 本来的做法会导致除零错误。所以 Photoshop 在这种情况下会直接把 color channel 设置为零。
  • 颜色比 α 大，这违反了前面提到的 pre-multiplied-α 对数据上界的限制。这种情况下二者的商大于一，Photoshop 把内部图层的 color channel 截取为 1，在 blending 的时候会乘以 α 值，最后的结果低于正确值。

没有办法能生成一个图层让 Photoshop 完成 r-blending 的功能。所以变通方法是生成第三个图层，使用 Photoshop 的 Add blending 模式（Linear Dodge），把上面丢失的 color 部分补回来。

上面左图是 rendering 结果被 Photoshop 当作 pre-multiplied-α 数据调入并转换为 unmultiplied 之后的数据丢失结果。右图是把 unmultiplication 转换中丢失的信息变成一个 Add-blending 图层。作为参考，这里附上生成 Add-blending 图层的 shader：

结论

虽然 α-blending 最原本的定义非常简单，但是每当在实际案例中涉及它的讨论总会有各种各样的 confusion。这篇 blog 从最原本定义入手。其目标是探讨一下这些 confusion 的来历。

最开始的讨论可以看出，α-blending 的原本定义并不符合简单的物理模型。目前的图像硬件的常用算法也不能和 α-blending 很好的兼容，为此提出了 pre-multiplied-α 这样凑合的方案。这就提出了一个疑问，这样一个充满缺陷的定义如何能得到广泛应用？答案是，其实得到广泛应用的并不是 α-blending，α-blending 只是以 Photoshop 为代表的各种软件的误导名词。

很多具有物理意义的场景其实采用的是我们命名为 r-blending 的方法。因为 r-blending 的公式恰好和 pre-multiplied-α blending 形式相同，所以它的应用经常调用硬件和系统库中叫做 pre-multiplied-α 的方法。但是在这种场景中引入 α-blending 和 pre-multplied 这两个概念没有任何好处，只能增加 confusion。

而重量级的工具比如 Photoshop，依然顽固的只采用 α-blending 概念。习惯的力量如此强大，以至于 α-blending 和 pre-multiplication 依然在制造 confusion 和不必要的工作。

脚注：

  1. 称为理想的 lambertian 表面。
  2. 由于只有漫反射，光源的方向不重要。
  3. 在此设定下 α 并非微分属性，而是整体的体积属性。对于类似薄片的「色层」来说，这是可以接受的简化。
  4. C 是频谱的函数。
  5. 从这里开始我们用「图层」来代替「色层」，因为我们的讨论的例子从一开始的单色层转变成接近实际的每个 pixel 颜色不同的图像。
  6. 在声称支持 pre-multiplied α-blending 的系统中，如果图层的 C’s 违背了小于 αs 有时会导致系统无法正常工作。下文讨论会提到。
  7. 可以称为 unmultiplication。
  8. 考虑到 Photoshop 大多数处理还是基于 8-bit，这种反复的乘除的精度损失也不小。

发表在 未分类 | Leave a Comment »

什么叫备份

2023/08/08

每隔一段不长的时间，就会看到网上有人抱怨：

因为外接存储设备的质量问题，我丢失了大量数据！

有时候这种抱怨还会成为一个大新闻。但是，劣质的存储设备只应该消耗额外的金钱和时间，绝对不应该消灭你的数据。如果你对自己说，这次劣质的设备让我得到了教训，要用好的设备来备份，那你不懂什么叫「备份」。

Restorability

首先，备份绝不只是定期把数据写到另一个存储器上。备份的目标是未来一旦发生灾难可以恢复数据。所以备份的第一指标是 restorability。如果你用一个 script 每天定期把数据 dump 到另一个 storage 上，然后就甩手什么都不管了，这不叫备份，这叫 dump to cold storage。有多少人的数据都好几天读不出来了，还浑然不知。一个基本的备份过程要求：

  1. 把数据写到备份 storage 上。
  2. 检查写入的数据是否能成功读出。

当然，在合理的成本约束下第二步不可能把所有备入的数据再全部读出，只能是随机抽检。对于个人用户来说，随机抽一两个文件打开即可。后面会定量分析这么做的结果。假设你的设备每月失败率是 5%。那么有了第二步，你的数据丢失率才是 5%。否则，假如你一年后才想起来 restore 数据，那么你看到的失败率会是 1 – (1 – 5%)12 = 46%。也就是说，一半可能你的数据已经丢了。两年后数据丢失几率上升为 70%。

Redundancy

单靠关注 restorability 这个概念本身，还不是健全的备份机制。因为发现备入的数据无法读出时，除非运气特别好（此次失败只影响了刚刚写入的数据），否则在同一个 storage 上的历史数据很可能丢失。

这样就要涉及 redundancy。把上面的备份过程扩展为：

  1. 把数据写到备份 storage A 上。
  2. 检查写入 A 数据是否能成功读出。
  3. 把数据写到备份 storage B 上。
  4. 检查写入 B 数据是否能成功读出。

这样备份的初始成本扩大了一倍 —— 因为必须购买双倍容量的 storage。好处是即使在第 2 步或者第 4 步发现读出失败也并不会丢失数据。这里做一下分析。假设一个设备在两次备份之间的失败率是 5%。那么在上面的流程中，真正丢失数据的几率是 (5%)2 = 0.25%。失败率下降为原来的 1/20！现在假设你不小心买了两张烂盘，失败率高达 20%，那么丢失数据的概率为 4%。可以看到，虽然 storage 的质量下降了很多，但是数据丢失的概率比只用一张 95% 可靠度的 storage 还要更低！

现在我们进一步扩展上面的过程：

  1. 把数据写到备份 storage A 上。
  2. 检查写入的数据是否能成功读出。
  3. 把数据写到备份 storage B 上。
  4. 检查写入的数据是否能成功读出。
  5. 等待备份周期的一半，检查 A 和 B 的读出。

上面假设我们用的两张烂盘在备份周期失效的概率为 20%。那么这里在第 5 步它们的失败概率为 10%。数据丢失的概率降为 1%！而如果用备份周期失败率 5% 的盘，失败率降为 (5% / 2)2 = 0.0625%。

但是这个流程有一个要点，每次发现设备失败的时候，必须立刻购买新的设备补上，否则整个备份机制的可靠度立刻退化为单张盘的可靠度。

抽查力度

前面提到检查 restorability 的过程出于成本考虑只能部分抽检。假设有 20% 的几率检查。拿可靠度 80% 的设备来说，查不出实际问题的概率为 10% x 20% = 2%。这时系统退化为单盘可靠度（而用户不知道）。实际增加的数据丢失概率为 20% x 2% = 0.4%。整个流程的失败率为 1.4%。而如果是可靠度 95% 的盘，整个流程失败率为 0.0625% + 2.5% x 20% x 5% = 0.0875%。

备份可靠度

整体而言，一个备份流程的可靠度受到这些因素影响：

  • 单个设备可靠度。
  • 冗余设备的数量。
  • 更换失败设备的速度。（本文还没分析过这个元素，读者可以当作练习。）
  • 检查 restorability 的频度。
  • 检查 restorability 的力度。

个人用户若选择自行备份数据，就要了解隐含的时间和器材成本。至少要准备双份冗余。至少在每次备份时抽检 restorability。尽量保证抽检有 80% 以上的可靠度。如果单月失败率 5% 的设备每 1.5 年可能期望失败一次，0.25% 意味着 33 年期望失败一次。而如果做到每半个备份周期多检查一次读出，0.0875% 就意味着 95 年可能期望失败一次。

但事情的另一面是持续投入，80% 可靠度的设备，平均五个月要更换一个 storage。95% 平均一年半要更换一个设备。容量越大的设备，可靠度必然更低。所以，当你看到单个 1T 硬盘价格的时候，不要再以为那是你备份 1T 数据的成本，整个备份机制成本至少是它的数倍以上。

发表在 未分类 | 1 Comment »

Await：从 Swift 到 C++

2021/06/16

上周三（6/9）早上醒来，发现全世界都在赞叹 WWDC 里宣布的新版 Swift async/await 特性。看了几条信息隐约说是基于 coroutine。尽管从去年起因为对 Apple Silicon Mac 迁移的失望已经把个人项目向 Windows 平台转移，但看在当年研究 Lua coroutine 和 Lisp continuation 下了很大功夫的份上，决定探索一下这个 Swift 语言新特性的细节。特别是在没有 VM 的语言上采用 coroutine 会有什么样的挑战。

这一看发现 Swift 并非仅仅给普通的 coroutine 库加上一点 syntax sugar 而已。这里要提一下，我最早看到的一条相关信息就是抱怨它只在最新的 iOS 15 上才支持。如果这个新特性真的只是普通 coroutine 库的语法糖，那这个抱怨是合理的。但其实并非如此。要解释这点，先回想一下最开始学 coroutine 的时候，一般的库或者 Lua 这样的语言文档如何给开发者展示第一个例子 [1]。在这个例子中会有 coroutine caller 和 coroutine 本身。前者是普通的 code flow，用 resume 来跳转到 coroutine。后者则用 yield 回到 caller。但 WWDC 的介绍视频里显然没有明确或者隐含提到这两者。所以第一步是找出 Swift 的实现和一般 coroutine 概念之间的联系。

一般概念与 Swift 实现

Swift 的 await 操作中止当前的 event-handler，而这个 handler 的 context 并没有丢失，可以在以后被恢复。所以 await 相当于 Lua 的 yield 操作。这说明了几点：

  1. 在 WWDC 视频中的例子里，coroutine caller 是 event-loop。视频并没有明确指出这一点，但是从 await 挂起当前 handler 之后可以处理其它 event 这点可以推断出来。
  2. 在 iOS 15 中，event-loop 调用 event-handler 不再是普通的函数调用。而是创建运行 event-handler 的 coroutine 并执行它。
  3. 视频的例子中，没有明确的 resume 操作。实际的 resume 操作隐藏在 event-loop 代码中。
  4. 在视频最后的例子中，continuation.resume() 并不是真的 resume 操作。它只是给对应的 coroutine 做上标记。而 event-loop 在随后的运行中会通过这个标记决定 resume coroutine。

要做到这几点，event-loop 的代码必须改写并用新版的 Swift compiler 重新编译。这就是只有 iOS 15 支持 async/await 的原因。以上是这个 Swift 语言特性和一般 coroutine 概念的对应关系。

Coroutine 的普及度

从上节可以看到，Swift 的 coroutine 的实现，至少在 WWDC 视频中呈现的场景，和 event-loop 紧密集成。我认为这个设计才是能真正发挥 coroutine 价值的关键，而且是以普通水平的程序员能接受的方式。在没有和 event-loop 紧密集成时，coroutine 虽然看起来炫酷，但在实际中处于「叫好不叫座 」 的局面。下面分析一下为什么缺乏 event-loop 帮助的 coroutine 难以体现价值，至少是难以让大多数程序员受益。

从模型能力来说，coroutine 的价值在于提供了独立的 call stack，并且切换开销比操作系统线程低。要体现它的价值就要充分利用其独立 call stack。在《Programming in Lua》中列举了 coroutine 的三种典型用例：iterator，consumer-producer，协作式多任务。 前两类需求用传统的没有独立 call stack 的方法解决并没有很大问题，并不值得引入 coroutine。

那么协作式多任务是 coroutine 最重要的应用场景吗？在多线程如此普及的时代，为什么需要协作式多任务呢？《Programming in Lua》里给出的解释是，协作式多任务可以把 non-blocking I/O 封装成为普通的 blocking 形式。在 2010 年左右，Lua 作者以 socket select 作为例子。虽然也勉强称为「non-blocking」，但这种传统风格的 I/O 并没有显示 coroutine 的价值。从 2013 年后，non-blocking I/O 的形式发生了很大变化，也脱离了 I/O 这个狭义范畴，变成了带有 completion closure 的 async function [2]。所以我们下面要讨论的 coroutine 应用是如何用它封装 async function。

在继续讨论 coroutine 之前，先说说 async function 本身的问题。它用 completion closure 来处理异步返回的结果。这样它的 continuation 就不能通过普通的 code flow 体现。如果要先后使用多个 async function 的话，就会导致 callback hell。现在设想一下：如果能把 async function 封装成某种形式的函数，在 coroutine 中调用这个新函数，它会调用原来的 async function。这个 async function 会立即返回 [3] ，然后新函数会 yield 当前 coroutine。这之后 coroutine caller 定期用某种方式查看 async function 的 completion closure 有没有触发，如果已经触发过就 resume coroutine；此时 coroutine 里接下来的代码就可以自然的处理 async function 的结果。我们可以把这种新的封装形式称为 coroutine-aware async，它可以让 coroutine 的正常 code flow 而不是 completion closure 来处理 continuation。

这种 coroutine-aware async 允许程序代码用普通的 code flow 调用 async function。看起来一切很美好。但我们还没有考虑一个关键问题，实现 coroutine caller 的复杂度。当某个 coroutine 因为等待 completion closure 被 yield 挂起的时候，我们希望 coroutine caller 能利用这个时间去执行其它有意义的任务。这就要求 caller 不能是普通的应用逻辑，而必须是比较通用的 scheduler。而编写 scheduler 并不是大多数程序员想要做，甚至不是有能力做的事情。所以这种 scheduler 一般都会封装在某种库或者框架中。如果这个库或者框架并不是全局掌管整个 app 运行模式的框架，那这个 scheduler 就只能在局部的特定领域使用。所以，对于大多数程序员来说，coroutine-aware async 很少能和他们接触的领域产生交汇。那么问题另一面是，为何不写一个掌管整个 app 运行模式的 coroutine scheduler？那么答案是，在绝大多数 app 中有一个天然的位置适合做这个 scheduler，就是 event-loop。但是 event-loop 被极少数代码垄断，典型的如 OS vender 自己的 UI framework，或者像 Qt 这样接管全局的框架才能做到。而这些垄断者之前并没有在 coroutine-aware 方面迈出步伐。

直到 WWDC 展示的下一版 Swift 提供了这个 scheduler。它的 async 就是 coroutine-aware async。这个新的语言特性是真正能让 coroutine 出现在更多应用代码中的关键。

尝试跨平台实现

赞叹了 Swift async/await 的设计之后，我面临一个挑战。Mac 作为个人计算平台的角色已经被全面向 Apple Silicon 迁移的战略断送。我自己的个人项目完全转向了 Windows 和 C++。最好能在 C++ 上实现 async/await 技术。

首先面临的问题是，Windows 并不像 macOS/iOS 那样大量使用带有 completion closure 的 async function 作为 APIs。好在我实现了一个简单的类似 libdispatch 的 NuoDispatch。只要能在非 main thread 上安全运行的代码都可以通过 NuoDispatch 改成 async function 形式。接下来就是 coroutine 本身的实现。

最先研究的技术是 C++ 20 引入的 co_await。看了之后大失所望。这个特性实现的是 stackless coroutine，就是说 coroutine 的范围只能是直接使用 co_await 的 function。我不明白 C++ committee 或者任何人怎么会在 2020 年还采用 stackless coroutine。编程语言中的 function 今天是一种封装和重用的机制，而不是控制 code flow 的机制。不能想象，本来应该放到第二层 function 中的代码为了用 co_await 必须放到上一层中。我想 C++ committee 设计 co_await 的时候脑子里一定在想 iterator/consumer-producer 这类的应用，设计出一个根本没法用于 event-loop scheduling 的废物特性。

接下来看了一些 stackful coroutine 的 C++ 实现。很多实现基于 POSIX context，不能支持 Windows。而且我个人对 「集成污染」比较敏感。 一番折腾下来，我开始想放弃这方面尝试。

退一步想想 await 配合 coroutine 的意义在于把 code flow 交还给 event-loop。如果不能用 context switch 的方式回到原来的 event-loop，还有没有其它的方式？Windows 的 event-loop 其实只有三到四行代码，而且本身在 call stack 上几乎没有 contextual data。所以答案是 Win16 时代的老技巧：再开一个新的 event-loop。我给 NuoBackgroundTask 添了两个新方法：

Resume() 在第一次执行时会把 NuoBackgroundTask::_work 交付给 background thread 运行。随后它每次被调用时会分发一次 event-queue 里的消息，让其它 event-handler 有机会运行，然后检查 _work 是否已经结束，并返回其状态。 Await() 的实现是简单的：

通过 Resume()，ModelViewerWindow::OpenFile() 从定义两个 completion closure 的方式变成了自然的 code flow。达到和 Swift async/await 在普通 event-handler 中使用同样的效果。几乎任何语言任何 OS 都可以受益于这种设计模式，而不再局限于最新的 beta iOS/macOS 和 Swift runtime。

再审视 Swift Async/Await

回头看 Swift 语言本身的 async/await，把通用的 stackful coroutine 引入 Swift，并与 event-loop 紧密集成。 这是非常聪明的实现 。但是再想一下，目前它也有很大的局限性。对 event-loop 的侵入式修改使老版本的 iOS/macOS 无法支持，对 runtime coroutine 实现的依赖使得 Swift 以外的语言无法使用。

既然 coroutine 和 event-loop 的结合才能降低 coroutine 的门槛让普通程序员接受，其实第二消息循环也可以做到，而且后者不需要依赖汇编代码，POSIX 特有的 API，或者 LLVM 特有功能。这种方式摆脱了 Swift，让 C++ 也能采用同样的自然 code flow 的设计。而第二消息循环对 root event-loop 的非侵入性让 iOS 15 和 macOS 12 以外的 OS 也能支持这个技术。

脚注：

  1. 后面关于 coroutine 的术语如果不加说明，都采用 Lua 的术语。
  2. 注意这里的 async function 指类似 iOS 14 和 macOS 11 之前的采用 completion closure 的 API 形式。和 async/await 中的 async 不是一回事。后文会把 async/await 中的 async 方式称为 coroutine-aware async。
  3. 这里指普通的 function return，而不是触发 completion closure。

发表在 C++, 软件开发 | Leave a Comment »

Exception Reconsidered

2020/12/24

我一直是 C++ exception 的反对者。《Programming in Lua（二）－ 异常与错误码》提到 Russ Cox 谈论 C++ exception 的所谓「根本缺陷」。我以前的认识是返回 error code 是最好的错误处理方式。

和返回 error code 不同，exception 会触发 call stack 的回退，从而失去了错误发生时的程序运行状态（指代运行状态的术语是 continuation）。这是我之前极力避免 exception 的最大原因。但是最近几年的实践里我发现即使不使用 exception 很多情况下也难以避免丢失 continuation。比如说，越来越普遍的 asynchronized APIs 让 continuation 在代码中的表达更加复杂，代码稍作简化就会丢掉 continuation 信息。另一个例子是，任何程序都无法避免 crash。在操作文件的过程中发生 crash，错误处理只能由下一次程序运行来完成，而 continuation 毫无疑问已经丢失。

如果使用 exception 并不是丢失 continuation 的唯一原因，就必须在假定 continuation 必然丢失的情况下进行错误处理。

计算机工程中减少对 continuation 依赖的方法是增加数据结构的能力。这点写过 parser 的人都会了解。实际上我以前提到过 exception 很适合关系数据库的 CRUD 操作的错误处理，那么在设计数据结构时把数据库的 two-phase commit 借鉴过来就可以了。当操作数据结构的时候，把要操作的部分（比如某个 tree 的一个 sub-tree，或者某个文件 folder）先复制一份。全部操作成功之后，才用这个拷贝替换原来的数据，只需保证这个替换过程是 atomic 的过程。通常的操作都能满足这个要求，比如指针赋值和文件目录的改名（而且后者是 crash-proof）。

我想 exception 在计算机工程里引起这么大的争议，和错误的教育是分不开的。基础理论很早就对 continuation 和数据的关系有深入的了解，而在介绍 exception 的文章里，谈到 exception-safe 仅仅等同于「正确的 pair 操作」。连 Russ Cox 之类的优秀工程师也会把这个教育问题当成 exception 机制的固有问题。SQLite 之类方案的存在一定程度上缓解了这个争议，不过更根本的方法是应该对常用的数据结构提供 copy-on-write 的复制机制。

发表在 C++, 软件开发 | Leave a Comment »

Phong Model and Physically-Based

2020/04/25

Phong model 大概是计算机图形领域最简单的材质模型。仅由三个 (组) 参数组成。Nuo Model Viewer 作为个人学习项目从实现 rasterization 渲染入手，自然最初只支持 Phong model。有个问题伴随着 Nuo Model Viewer 的扩展：是否要支持其它更复杂的材质模型？另一个相关问题是，如果 Nuo Model Viewer 支持 path-tracing，对于现有基于 Phong model 的模型是进行预处理转换成其它材质模型，还是在渲染中直接处理 Phong model ？

我准备在 Nuo Model Viewer 中实现 path-tracing 时发现手头大部分模型只有 Phong model 材质。更重要的是，计划实现的许多效果似乎不需要一种比 Phong 更复杂的材质模型。我决定在渲染算法中直接处理 Phong model 或者它的简单变种，因为可能有两个好处：第一是避免让代码更复杂去支持实际很少用到的材质模型；第二是避免直接照抄现有资料里对材质的处理，从而能发现渲染方法和材质模型集成的一些问题 [1]。

什么是「Physically-Based」？

首先把注意力从 Phong model 本身移开，从更宽泛的角度考虑材质模型在渲染方法中「可用」的标准。Path-tracing 渲染的方法和材质被称为 physically-based。渲染过程的 light tranport equation 可以说有比较严格的物理基础，但材质方面很难用简单模型直接模拟物理材料。 现今使用的 phiscially-based reflection models 的定义和真实世界材质的微观结构只有很弱的联系。所谓「弱联系」意味着图形学的 physically-based material 不代表「符合」真实世界，而仅仅代表「不违反」真实世界的某些限制。

最常见的 physically-based model 是 BRDF。满足「能量守恒 (energy-conservative)」和「光路可逆 (reciprocal)」两个限制的 reflection model 都可称为 BRDF。更「真实」的 reflection model 就是要满足这两个 BDRF 限制以外的更多限制。虽然很多介绍 path-tracing 的资料涉及了更「真实」的 reflection model，但几乎没有直接总结 BDRF 以外的限制。为了稍后能理解 Phong model 的局限以及如何修改让它能适应 path-tracing，把这些限制一起总结如下：

  • 能量守恒，对所有可能的 ω’，reflectance distrubtion 满足；
  • 光路可逆，满足 ；
  • 连续变化，如果观察真实材质时视角和光源的连续变化不会导致颜色的突变，那么虚拟材质的定义也要保持连续。
  • 边界条件，这条会在后面章节详细解释。

BDRF Normalization

现在回到 Phong model 本身。如果它能够直接或者在修改后满足上节列出的限制，就能适用于 path-tracing。在 Phong model 刚被提出时，计算机图形还通常只处理 singular 光源 (点光源或理想方向光源) 。这种情况下 Phong model 公式为：

这里的是出射光线与入射光线的理想镜面反射方向之间的夹角。因为后来提出的 micro-facet 模型以及实际观察的效果，在实际应用中已经被 half vector 和 normal 的夹角取代。本文后面也会改用，但目前的讨论中依然先用。

要适应 path-tracing，这个公式首先要改写成基于 reflectance distribution 的积分形式，从而不再局限于 singular 光源。并且我们希望改写后的形式至少满足 BRDF 的两个限制。首先，把相对光强值替换为有实际物理意义的 radiance。然后在式子中加入 normalization 系数和，下面我们分析如何对它们合理取值以满足 BDRF 甚至更多的 physically-based 限制。

在分析和如何取值之前先解决另一个问题。在上面式子中出现了作为分母的情况，所以必须对为零的情况做下面的特殊处理：

这违反了前面提到的「连续变化」限制 [2]。所以很早出现的对 Phong model 改动之一是去掉分母，变为 [3]：

这个变化说明为了让 reflection model 满足 phiscally-based 的某个限制，我们会作出并不深究真实物理根据的「粗暴」改动。现在来确定和的具体取值。这里先尝试只考虑「能量守恒」限制。假设材质只有 diffuse 部分 (即为零)，从以前的 blog 可以得出在不大于 1 的前提下，有：

用类似的方法分析，先假设为零，满足能量守恒的不等式为：

这里不妨设 ω‘ 与 normal 重合，因为可以使不等式左侧最大化。左侧变换为：

可以得出在不大于 1 的前提下，有：

需要注意的是上面的推导基于而不是今天业界常用的。基于的推导复杂得多。所以本文只用基于的推导展示大致思路，就不具体推导基于的模式。而且基于的模式中的精确取值很复杂，实际工程中一般取下面的近似值：

用代替的 Phong model 的变种称为 Blinn-Phong。经过 BDRF normalization 的 Blinn-Phong reflectance distribution 的完整公式为：

至此我们完成了修改 Phong 更加符合 physically-based 原则的第一步，BDRF normalization。在这个过程中有没有忽略或者违反了其它的 physically-based 限制，在后面会有更多的讨论。

Importance Sampling

为了在 path-tracing 过程中使 Monte Carlo 方法能更快收敛，需要在 path construction 过程中选择合适的 importance sampling。以前的 blog 里分析过，当 path construction 的采样概率分布为时 LTE 的 Monte Carlo estimator 为：

下面分别考虑 diffuse 和 specular 部分。对 diffuse 部分来说，只要让采样概率分布满足就可以让 estimator 简化。把一个 uniform 分布的随机变量转化为是非常简单的操作，这里不详细分析。

下面来分析 specular 部分。 Blinn-Phong model 只考虑 specular 的 estimator 可以直接写为：

关键在于找到合适的 来抵消。因为与 half-vector 相关，很难通过到入射光线的采样来抵消它。所以我们尝试用 sample half-vector 的方法来解决。有现成的办法 [4] 可以把 uniform 分布的随机变量转换为满足的随机量，根据概率分布的归一化可以得到 [5]：

根据和的微分关系，可以得出：

将上式代入之前的 estimator 公式，就可以得到 Blinn-Phong specular 部分的 Monte Carlo estimator 为：

边界条件

上面章节数学分析已经足够在 path-tracing renderer 里原封不动地实现 Blinn-Phong model。按照所述的方法 Nuo Model Viewer 做到了 path-tracing 和 rasterization 的效果几乎一致。

接下来我们当然想验证用这种实现能否完成更多 physically-based 效果。在 Nuo Model Viewer 的实际测试中，间接光照和体积光源的效果都不错。那么在 path-tracing 中经常被提及的镜面反射效果方面，Blinn-Phong model 的表现如何？

现在暂时脱离对「镜面效果」的分析，而去考虑如何衡量一个 reflectance distribution 的数学描述是否更好的符合物理实际。我们几乎不可能实际测量真实世界的物体表面在整个球面坐标上任意两个方向的光线反射能量比，也不可能随心所欲地构建物质来验证任意参数的 reflectance distribution 函数。但我们有可能做到两件事：第一，用实验测量或者严格的物理理论来得到特定方向上的光线反射能量；第二，把实际物质表面的某种特定性质对应到 reflectance distribution 参数的某个特定取值。这样就可以比较测量值或理论计算值是否和对应参数的 reflectance distribution 在特定方向的值足够接近。这就是用「边界条件」来衡量 reflection model 的质量。

回到「镜面效果」的问题。在真实世界里随便选择一个实际物体的表面，我们没法直接得出其对应的 Blinn-Phong 或者其它 reflection model 的参数。但是对于真实世界中非常光滑的接近镜面的表面我们可以做到。对于基于 micro-facet 模型的 reflection model 来说，「非常光滑」表示 micro-facet normal 的分布不再是连续范围，而是等于宏观的 surface normal。对于 Blinn-Phong model 来说，这表示的参数 m 为无穷大。

另一方面，我们可以在真实世界中通过物理理论分析和实验测量来得到光在光滑表面上的反射能量。通过 Fresnel equation 分析和测量的验证可知镜面反射方向出射光和入射光随入射角的变化规律。当从 0 开始增加时，在很大范围内出射光的 radiance 和入射光之比接近一个小于 1 的常数，在接近 90 度时这个比值会急剧上升，在 90 度时为 1。在物理学上把这个比值相对的函数称为 Fresnel reflectance，用表示。

现在回去检验 Blinn-Phong model 是否符合镜面反射下关于的「边界条件」。当 m 无穷大的时候其 reflectance distribution 是一个冲击函数，这时 Monte Carlo 的采样方向不再随机分布，而是固定在理想反射方向。其 estimator 就是积分的确定值。

而根据物理分析，我们期待的理想镜面采样值应该是：

上面的 reflectance distribution 的计算值中的导致了在边界条件下显然不符合实际的物理状况，连近似都谈不上。说明 Blinn-Phong model 不能胜任在 path-tracing 中实现镜面效果。Nuo Model Viewer 的测试结果是镜面反射的光强过低。因此我们要寻找新的符合镜面「边界条件」的 reflection model。我们希望在的情况下这个模型的 LTE 积分和上面期待的采样值近似或者相等。

但是，先等一下！既然我们希望采样值是上面的形式，那还用求出 reflectance distribution 吗？直接把这个采样值作为 Monte Carlo 过程的 estimator 不就可以了！确实如此，只不过还需要对它做个小改动。上面的式子并不能在接近 0 的时候连续的减少为 0，以此它依然有最初 Phong model 在处不连续的缺陷。考虑到这种不连续通常在观察角度 (也就是) 比较小时影响明显，所以我们把 estimator「粗暴」地改为：

从这个 estimator 可以反推出 specular reflectance distribution 为：

而我们可以在《Physically-Based Rendering》介绍的几种 model 中发现，其中的 Fresenel Blend model「恰好」符合上式。这大概也是它得名的原因 —— 与其说是通过完整物理模型推导出来的，不如说它只是从这单个实际物理特性出发，考虑 micro-facet 模型共有的与的微分关系，为了满足「镜面」边界条件反向凑出来的模型。

前面提到过给定材料的光滑表面的在从 0 开始的一个很大范围内都等于某个小于 1 的常数。我们可以把用作这个常数。对于大多数金属，其光滑表面的接近 Schlick 方法：

如果把上式推广到「不绝对光滑」的 micro-facet 模型表面，应该由与 micro-facet normal 相关的夹角取代。同时，因为 specular 部分的取值大于 Blinn-Phong model，Fresenel Blend 的 diffuse 部分要依据「能量守恒」作出调整。

Physically-Based Rendering

本文讨论了 Phong model 如何经过必要修改从而应用于 path-tracing。经过修正的 BRDF Blinn-Phong 可以用于 path tracing 的 importance sampling。但它也有不能实现镜面反射的局限性。

新选用的 Fresenel Blend model 满足镜面的边界条件。同时它的 reflectance distribution 可以适用于任意的，也就是任何 micro-facet model。所以类似于 Blinn-Phong，基于Fresenel Blend model 的 Monte Carlo 过程依然可以采用的 path construction 方法。这样 Nuo Model Viewer 只需要单一的 importance sampling 代码。

和 Blinn-Phong 一样，Fresenel Blend model 也由三个 (组) 参数定义。可以直接把前者的，和 m 套用到后者上。但这样直接套用的结果当然和 Blinn-Phong 本身的效果不同。在无需明显镜面效果的模型上 Nuo Model Viewer 依然采用 Blinn-Phong model 来体现设计本意。需要镜面效果的部分通常是地面，特别是和真实图片 blending 时采用的 virtual ground plane。Nuo Model Viewer 在这部分采用 Fresenel Blend model。

脚注：

  1. 这也秉承了我一贯不喜欢用现成实验环境的习惯。
  2. 对 reflection model 的积分通常只考虑上半球，所以 naive 的想法是取值造成的不连续性似乎无关紧要。但不要忘记，只考虑上半球的原因正是因为假定在的条件下。所以必须避免处的不连续。
  3. 因为去掉分母使被积函数整体连续，并且在时总为零，所以在只考虑上半球的前提下可以去掉其中的 max 函数。
  4. Diffuse importance sampling 可以看作此方法在 m = 1 时的特例。
  5. 此处推导与上文 specular 部分的 BDRF normalization 方法类似。

发表在 软件开发 | Leave a Comment »

单元测试和个人技能成长

2020/04/17

最近看到个对单元测试的看法：

单元测试是预防错误的主要手段。如果一个团队所在的领域对错误的容忍度高，而其市场需要 move fast，就 (暂时) 不用有单元测试；反之，若所在领域对错误容忍度低，那么重视实践单元测试的团队会取得优势。

然而，单元测试并不是「预防错误的主要手段」。首先单元测试并非全部测试。除了单元测试，还有组件测试，系统整体的人工测试，自动化的整体测试等等。团队资源应该在所有测试类型间合理分配，而不是预设单元测试最重要。其次，错误预防的关键点在于 escape to user 而不是 commit to repo。也就是说很多非测试技术，比如 Git 的合理 branching 策略和 back tracking 也可以更合理的成本降低错误。从最终结果的角度来看，若先不考虑 escape to user 造成的公开影响和修复 bug 的成本，系统整体的人工测试就可以发现所有错误。如果把软件开发的概念套用在流程设计上，整体人工测试是开发流程的基本功能，而其它方法都是开发流程的「优化」。那么可以想到关于优化的老话：「Premature optimization is the source of all evil.」 优化的前提是 profiling。制定流程应该把「只有整体人工测试」作为缺省情况，根据执行的实际结果谨慎加入其它技术。

说到这里谈谈这篇 blog 的真正重点。我之前涉及单元测试讨论的 blog 有好几篇，所以并不想再写一篇去扩展甚至重复以前的观点。这里我想到的不是分析的结论，而是分析这些看法的手段。最开始引用的看法把缺乏单元测试的视为一种「技术债务」而不是可以在团队中合理分析执行的长期策略。这是个错误的归类，而由这个错误可以想到技术人员如何思考自己的技能成长。

现今是「纯技术」有所贬值的时代。当年 Paul Graham 用 Lisp 作出网站卖得 5000 万美元而鼓吹了很久 Lisp。但回过头去看 Lisp 已没那么神奇。很多通用技术已经被成熟的模块甚至 AI 部分取代。技术人员需要思考的是有什么和技术密切相关但又不是「纯技术」的东西，可以帮助发展个人技能。对「技术债务」的理解和评估恰恰是技术人员可以体现不可替代性的重要项目。认清团队技术储备中哪些是资产，哪些是债务，如何合理的偿还或者重组技术债务，这些是和管理财务债务一样重要的技能。

发表在 软件开发 | Leave a Comment »

一次性代码和坚固的基础

2019/10/13

我对「技术债务」的态度和像对财务债务一样「中立」。借入债务以求发展是必要的，只要在 accounting 里确实把它标成「债务」。债务不断积累时要寻求机会逐步清除它们。比如说对还算能运行的代码进行 refactor。

这会遇到一种反对意见：这段代码估计一两年以后就要废弃了，何必费力气？只要修修补补撑段时间就好了。

其实我的经历是被这么评价的代码反而往往会跟随一个团队十几年。另一方面，有些被寄予很高期望，计划会被使用很多年的代码却连一次正式使用的机会都得不到就被抛弃了。

其实这很正常。把两种预测反着理解就好。被人说「一两年以后就要废弃了」的代码若依然会被写出来，就说明有现实的需要，已经能给公司和团队带来正面的资源。这样的东西要被推倒重来是几乎不可能的。而「计划会被使用很多年的代码」往往是基于长远的愿景而缺乏当前的盈利模式，最后如果不能发现盈利的契机就被放弃。

发表在 软件开发 | Leave a Comment »

一张 WWDC 幻灯片

2019/04/04

之前的 blog 里提到过，尽管早有愿望学 ray tracing，但 2018 前半年总提不起兴趣动手。六月 Apple WWDC 2018 里关于 ray tracing 的 session 成为我第一次真正接触 ray tracing。望着讲台上削减至极的幻灯片和 speaker 超快的解说，我想这似乎并不难，大概下周给同事总结 WWDC 时就可以自己解释这个问题。

实际上到现在过了十个月，才能说大致理解了这张幻灯片的数学原理。一个简单的 demo 固然能推进学习的进度，但是也可能引入误解。

渲染方程

上篇《 Wavefront OBJ 与 Monte Carlo 》第一次尝试总结对 ray tracing 的理解。其中以下面的积分式求 radiance (后面称该积分式为，其中 n 表示积分层数)：

但根据渲染方程到达 camera 光线的 radiance 并非，而是：

这就是渲染方程的 light transport equation 形式。只是整个 LTE 中的单个 term，甚至没有明确的物理意义和常用名称。一般将其理解为光源经过 n 次反射/折射后对最终 radiance 的贡献。例如 n 取一时表示光源直接射入 camera，取二表示 direct lighting。

也就是说，上篇 blog 将直接作为 Monte Carlo 方法的求解对象的分析有些粗糙，需要修正为更严密的解释。

随机过程与「物理模拟」

在应用 Monte Carlo 方法分析之前，先说一下 Monte Carlo 方法的随机过程和 ray tracing 物理意义的关系。

当用简单例子 —— 比如说一元函数 —— 来说明 Monte Carlo 方法时，很明显会把它理解为一个抽象数学工具。把它应用在 ray tracing 问题时却容易误认为 Monte Carlo 方法的 sampling path 在模拟物理光线。如果在分析 ray tracing 问题之前没有把「path 不是光线」这个座右铭刻在脑子里，思维很容易走入歧途。

之所以 path 容易被误认为在模拟光线，是因为二者有些似是而非的相似性。最为显著的一点是，在定义渲染方程时，确实是以光线的物理特性为基础。但是最终定义得到的 LTE 的积分形式表明 radiance 的分布达到了 equilibrium 状态。这是统计上的确定状态，单条光线的特性已经被抛弃。之后对这个积分式采用的 Monte Carlo 方法是一种纯粹人造的随机过程，path 是纯粹抽象的随机取样。为了更准确的强调这点，本文描述的这种 Monte Carlo 求解 LTE 的方法不再被称为 ray tracing，而是叫 path tracing。

这里要提到的关于 Monte Carlo 容易被误解的最后一点是 estimator 和积分形式的对应和区别。Estimator 是随机变量，其数学期望等于它所对应的积分式的值。因此 estimator 和积分形式绝不能同时出现在一个公式中。不同随机过程产生的 estimator 也不能在一起运算。看起来很愚蠢，但我不知道反复卡在这个误解上多少次了。就在写这篇 blog 的过程中都曾经把两种形式写在一个式子中。

忽略光源位置的 Path Construction

回到之前的问题：需要通过 Monte Carlo 方法求解的是整个 LTE，而不仅是单个。

在 Monte Carlo 方法中只要取样足够多，最终结果的正确性和 path 的构建方法没有关系。不妨先讨论在构建中完全不考虑光源位置，也就是单纯依靠 reflection sampling 的方式。Reflection sampling 可以采用任何随机概率分布，比如 uniform sampling，当然更常见的做法是根据 BRDF 做 importance sampling。

根据上篇 blog 中的 estimator 可以推导出 LTE 的 estimator 为：

根据常识可以假定自发光物体表面的为零 —— 光源本身不反射任何其它来源的光线。所以构建过程遇到第一个自发光物体就结束。并假定在光源之前的遇到的所有表面点的都为零 —— 普通材质不发光。在这些条件下，每条 path 的 LTE estimator 值只剩下一个 term：

其中 c 表示遇到光源时的路径长度。代码实现可以给 c 设置上限，达到上限依然没有遇到光源就认为这条 path 的 LTE estimator 为零。由此可以看到仅用 reflection sampling 构建 path 时上篇 blog 的结论依然成立，仅仅是原来的 n 被意义更加准确的 c 代替。

考虑光源位置的 Path Construction

但是，仅仅依靠 reflection sampling 构建 path 与光源相交的几率很低，结果的收敛速度很慢。因此大多实现在构建时会将最后一段 path 的终点取在光源表面上。这样的方式中 path 不是随机遇到光源终止，而是被「强制」结束，也就是说 LTE 不再作为整体在 path space 中被随机采样，只能为每个执行独立的 Monte Carlo 过程来分别近似积分。因此虽无直观的物理意义，但仍是 path tracing 中的重要概念。

每个的 estimator 如下：

这里的表示物体表面 reflection sampling 的概率分布。表示最后一段向光源表面取方向的概率分布。如果在表面积为 A 的光源上做 uniform sampling，则有：

每个的 estimator 应该由不同而且相互独立的 Monte Carlo 过程取得，各自收敛的数学期望近似值才可以相加。但在实际工程中，通常用下面的近似式作为一个整体的 estimator。

这里的「取巧」之处在于的 estimator 前 n-1 个采样点和的 estimator 的采样点相同，在本该分别采样的多个独立随机过程中引入了 correlation。但是通常认为这对结果的影响可以忽略。其 path 构建过程相当于从 camera 发出的 path 每次遇到物体表面就随机产生两条 path，一条强制射向光源表面上的随机点，另一条通过 reflection sampling 而得。

回顾和比较

经过上面的分析之后，可以看到仅仅依靠 reflection sampling 的方法数学上更简单，实现也更容易。所以有些 ray tracing 的介绍材料 —— 比如《 Ray Tracing in One Weekend 》—— 就采用了这种方式。但这种方式存在一个陷阱，就是容易让人误认为 Monte Carlo 方法是物理模拟。一些材料出于「形象化」考虑也确实如此误导解释。WWDC 的 demo 没有采用这种方式，我读过其代码之后第一件事就是误打误撞把它改成了只有 reflection sampling 方式，也是潜意识里向「物理模拟」靠拢的体现，这个思路可能歪打正着写出基本功能，但要想进一步改进代码就会缺乏理论基础。

考虑光源位置的 path construction 是高级 ray tracer 的通常做法。它的难点在于实现的近似简化。实际代码往往不会真正独立地执行多个随机过程，而是如上所说通过共享随机采样用一个随机过程近似多个 Monte Carlo 过程。本来多重积分用 Monte Carlo 方法近似就是比较难理解的过程，再把多个独立的 Monte Carlo 过程近似成一个随机过程就更增加了难度。WWDC 的 demo 采用的基本是这种方法。但是在材质和光源上都做了进一步简化。特别是光源采样时完全忽略了对的处理。所以将其改成只采用 reflection sampling 方式之后和原来的 demo 并不等价。在理解其中的数学解释之前，渲染结果的差异一直让我困惑。我曾经以为 WWDC 的 demo 起到了带初学者入门 ray tracing 的作用，其实它的用途仅仅是给真正理解 path tracing 的老手展示 GPU 加速功能。

发表在 软件开发 | Leave a Comment »

« 以前的文章